Dimensionality Reduction and the Singular Value Decomposition
Dimensionality Reduction
One common way to represent datasets is as vectors in a feature space. For example, if we let each dimension be a movie, then we can represent users as points. Though we cannot visualize this in more than three dimensions, the idea works for any number of dimensions.
One natural question to ask in this setting is whether or not it is possible to reduce the number of dimensions we need to represent the data. For example, if every user who likes The Matrix also likes Star Wars, then we can group them together to form an agglomerative movie or feature. We can then compare two users by looking at their ratings for different features rather than for individual movies.
There are several reasons we might want to do this. The first is scalability. If we have a dataset with 17,000 movies, than each user is a vector of 17,000 coordinates, and this makes storing and comparing users relatively slow and memory-intensive. It turns out, however, that using a smaller number of dimensions can actually improve prediction accuracy. For example, suppose we have two users who both like science fiction movies. If one user has rated Star Wars highly and the other has rated Empire Strikes Back highly, then it makes sense to say the users are similar. If we compare the users based on individual movies, however, only those movies that both users have rated will affect their similarity. This is an extreme example, but one can certainly imagine that there are various classes of movies that should be compared.
The Singular Value Decomposition
In an important paper, Deerwester et al. examined the dimensionality reduction problem in the context of information retrieval [2]. They were trying to compare documents using the words they contained, and they proposed the idea of creating features representing multiple words and then comparing those. To accomplish this, they made use of a mathematical technique known as Singular Value Decomposition. More recently, Sarwar et al. made use of this technique for recommender systems [3].
The Singular Value Decomposition (SVD) is a well known matrix factorization technique that factors an m by n matrix X into three matrices as follows:
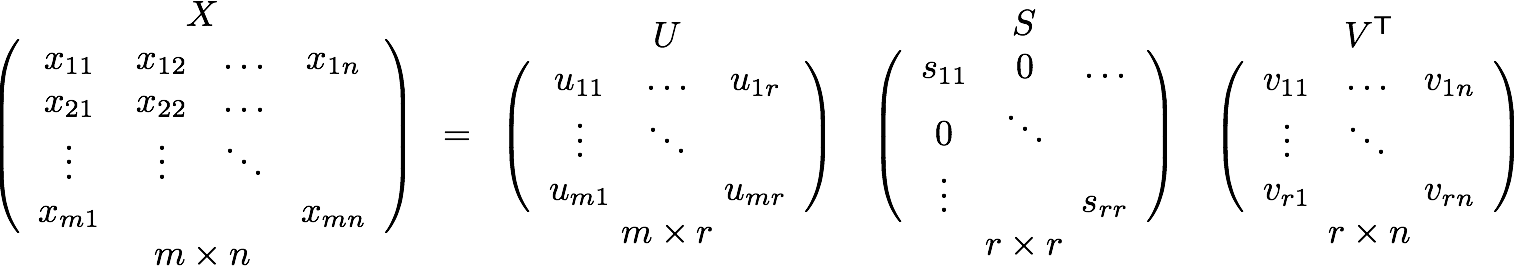
The matrix S is a diagonal matrix containing the singular values of the matrix X. There are exactly r singular values, where r is the rank of X. The rank of a matrix is the number of linearly independent rows or columns in the matrix. Recall that two vectors are linearly independent if they can not be written as the sum or scalar multiple of any other vectors in the space. Observe that linear independence somehow captures the notion of a feature or agglomerative item that we are trying to get at. To return to our previous example, if every user who liked Star Wars also liked The Matrix, the two movie vectors would be linearly dependent and would only contribute one to the rank.
We can do more, however. We would really like to compare movies if most users who like one also like the other. To accomplish we can simply keep the first k singular values in S, where k<r. This will give us the best rank-k approximation to X, and thus has effectively reduced the dimensionality of our original space. Thus we have
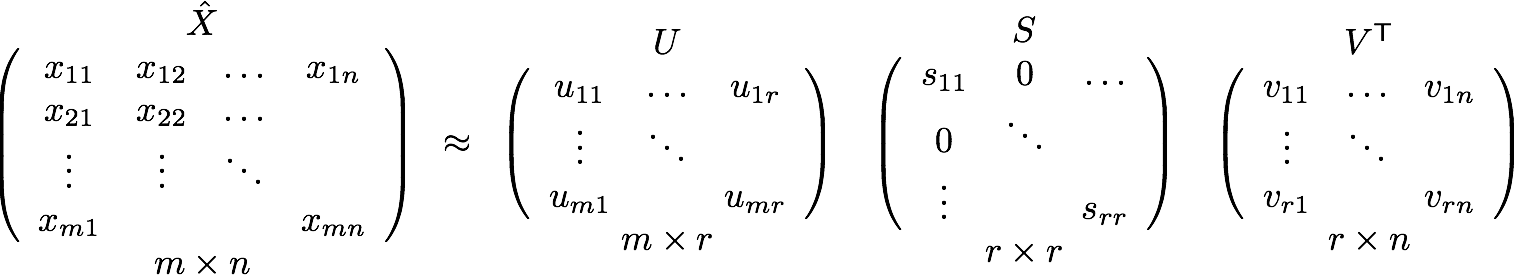
Recommendations with the SVD
Given that the SVD somehow reduces the dimensionality of our dataset and captures the "features" that we can use to compare users, how do we actually predict ratings? The first step is to represent the data set as a matrix where the users are rows, movies are columns, and the individual entries are specific ratings. In order to provide a baseline, we fill in all of the empty cells with the average rating for that movie and then compute the svd. Once we reduce the SVD to get X_hat, we can predict a rating by simply looking up the entry for the appropriate user/movie pair in the matrix X_hat. Further details can be found in [2,3].
Updating the SVD
One of the challenges of using an SVD-based algorithm for recommender systems is the high cost of finding the singular value decomposition. Though it can be computed offline, finding the svd can still be computationally intractable for very large databases. To address this problem, a number of researchers have examined incremental techniques to update an existing svd without recomputing it from scratch [1,4]. We looked at a method proposed by Matthew Brand for adding and modifying users in an existing SVD [1]. Brand focuses on so-called rank 1 updates, where a single column is modified or added to the orignal matrix. Formally, given the singular value decomposition of a matrix X, we want to find the singular value decomposition of the matrix X+abT, where a and b are column vectors.
The full derivation of Brand's method is beyond the scope of this document, but we will provide a brief discussion of the algorithm. Given the SVD X=USVT, let m=UTa, p=a-Um, p=sqrt(pTp) and P=p/p. Similarly let n=VTb, p=b-Vn, q=sqrt(qTq) and Q=q/q. Then we first find the singular value decomposition U'S'V'T of the matrix
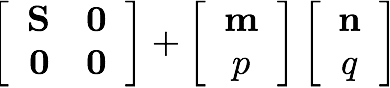
Then the svd of our new matrix is given by
Since we can use the low rank approximations of U, S, and V, this algorithm is quite fast, and Brand shows that the entire SVD can be built in this manner in O(mnk) time, where m and n are the dimensions of the matrix and k is the reduced rank of the approximation.
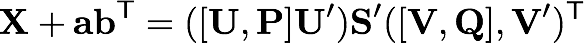
Extensions
The idea of reducing the dimensionality of a dataset is not limited to the singular value decomposition. While SVDs provide one of the most theoretically grounded techniques for finding features, there are a number of approximation algorithms that can be used on very large datasets. We did not explore this area in great depth, but we did use a method proposed on the Netflix forums by simonfunk and implemented in C by timelydevelopment. We ported this code to Java and tried it with both the Netflix and Movielens datasets. The fact that this algorithm performed the best among all of those we tried suggests that dimensionality reduction is a powerful idea that would be worth exploring in the future.
References
[1] M. Brand. Fast online svd revisions for lightweight recommender systems. In Proceedings of the 3rd SIAM International Conference on Data Mining, 2003.
[2] S. Deerwester, S.T. Dumais, G.W. Furnas, T.K. Landauer, and R. Harshman. Indexing by latent semantic analysis. Journal of the American Society for Information Science, 41(6), 1990.
[3] B.M. Sarwar, G. Karypis, J.A. Konstan, and J.Reidl. Application of dimensionality reduction in recommender system - a case study. In ACM WebKDD 2000 Web Mining for E-Commerce Workshop, 2000.
[4] B.M. Sarwar, G.Karypis, J.A. Konstan, and J. Reidl. Incremental singular value deocmposition algorithms for highly scalable recommender systems. In Proceedings of the Fifth International Conference on Computer and Information Technology (ICCIT), 2002.