Decimation
by Ben Anderson
We now have produced highly accurate geometric models of the surface we
are reconstructing. However, we have not considered how efficient
these models are. By efficient, I mean are we representing the
data using the fewest possible triangles to produce our shapes (this is
important because not only does fewer triangles mean shorter rendering
times, but in the case of the full human dataset, it means avoiding
blowing out memory).
Unfortunately, the answer to this is a resounding no.
Consider this. In areas of low curvature, we should only need a
few triangles to represent the original shape. In fact, the case
of a flat, rectangular surface, we should only need two:

However, using marching cubes, we will in fact produce two triangles
for every cube intersecting this surface (because we only triangulate
within the cubes):
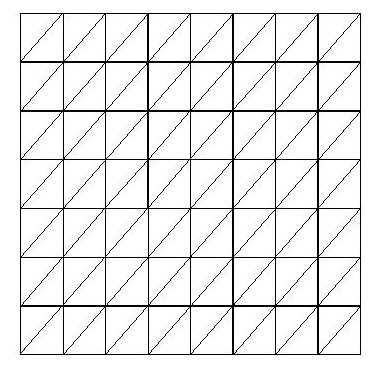
This is because for every cube intersecting the surface, marching cubes
must produce a triangulation. These triangulations consist of 1-4
triangles, and thus the entire surface will maintain roughly the same
triangle density regardless of curvature. Surface grower and
other triangulation methods which rely on point clouds also fall into
this trap because they will triangulate the entire cloud, and unless
the cloud density is lesser in areas of low curvature, triangle density
will be unaffected by surface curvature.
Decimating a triangle mesh is the act of removing triangles in such a
way that the overall original shape of the mesh will be maintained
intact. To do this, vertices are removed if doing so would not
produce much "error" where error is defined differently depending on
the type of vertex, but the basic meaning is "the amount by which
removing the vertex changes the original shape." A good decimator
would take the second shape above, and turn it into the first.
Lorensen, Schroeder and Zarge[3]
identify a means of doing this:
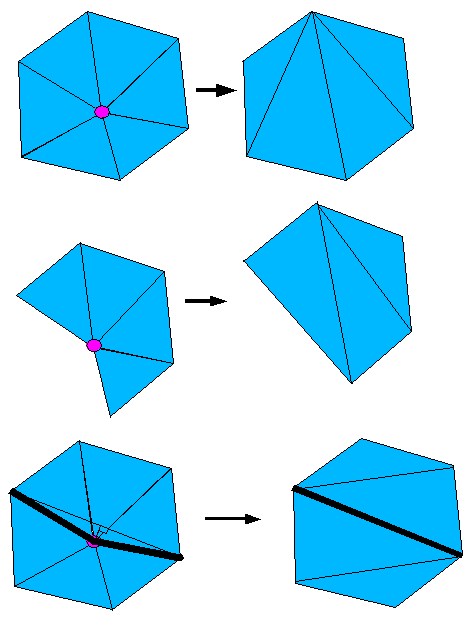
First they classify each vertex into one of three categories:
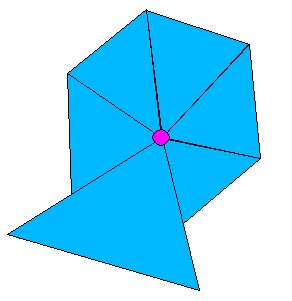
Complex, Simple and Boundary vertices. A complex vertex is part
of multiple triangles, at least one of which contains a vertex not
shared by any other triangle containing that vertex:
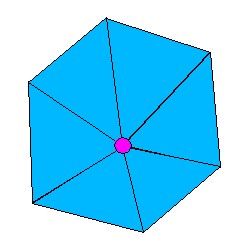
A simple vertex is one completely surrounded by other triangles all of
which share their outside vertices with each other:
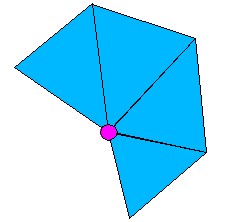
A boundary vertex is one which lies on the boundary of the object (ie,
on the lip of the foot in the cut-off example images):
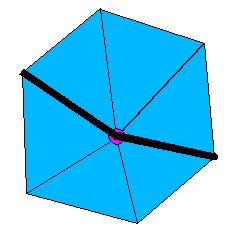
Simple vertices can further be classified as interior edge vertices or
corner vertices if two or more of the triangles containing them and
bordering each other have particularly sharp dihedral angles compared
to each other (steep is a user defined parameter). These edges
are called "feature edges" and exist when adjacent triangles come
together at sharp angles. Vertices containing two feature edges
are classified as "interior edge" vertices and vertices with three or
more feature edges are called "corner" vertices.
Interior edge:
Corner:
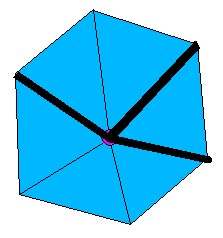
Of all these classifications, only complex and corner vertices are left
alone. Complex vertices are left alone because of the difficulty
in re-triangulating the whole left by removing them and the triangles
they are a part of, corner vertices because they often define
significant features of the shape.
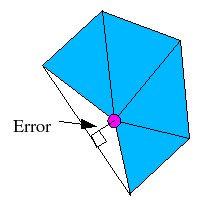
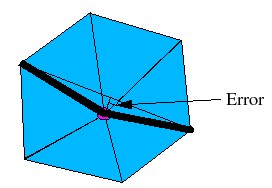
Once we have classified a vertex, we must then determine the error
removing it would produce. For simple vertices, this is defined
as the distance of the vertex from the "average plane" of the triangles
which contain it. The average plane is defined as the plane whose
normal is the average, weighted by size, of the triangles containing
the vertex, and containing the point obtained by averaging the
surrounding vertices. This looks something like:
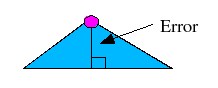
The error for a boundary vertex is the distance of that point to the
line defined by its neighboring boundary vertices or:
And similarly, the error for an interior edge vertex is the distance of
that point to the line defined by the two vertices lying on the edge:
Once a vertex is removed, all the triangles containing it are removed
as well. This leaves a hole which must be retriangulated.
This may be done by a variety of means, but the means used in the
literature, and by our implementation is a recursive loop-splitting
algorithm. What this means is that while there are more than
three vertices in the hole, two non-adjacent vertices are chosen for a
split. Then each side of the split is recursed on. The two
vertices that are chosen are those two which result in the largest
"aspect-ratio" or the ratio of the distance of the closest vertex to
the split plane over the length of the split line. The split
plane is the plane perpindicular to the average plane running along the
split line. Each split is also checked to make sure that all
vertices on either side of the split line are on the same side of the
split plane as all other vertices on that side. For interior edge
vertices, the first split is always between the two interior edge
vertices. If this all sounds complicated, it is. Resulting
retriangulations look like:
We learned about decimation at almost the last minute, and as such our
decimator class is somewhat incomplete. It currently only removes
simple vertices, and produces occasional artifacts in the form of
missing/botched retriangulations. It also runs relatively
slowly. However, once the artifacts are fixed, implementing both
speed improvements, and removing boundary and interior edge removals
are relatively easy tasks. Here's an example of the decimator at
work, and of one of its artifacts:
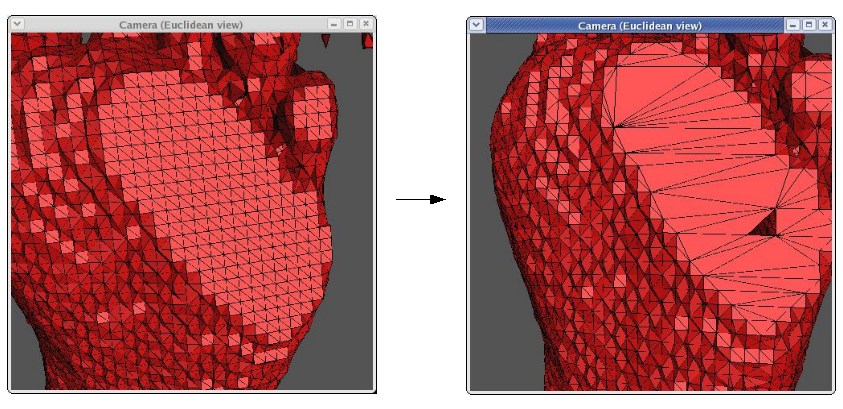
You'll notice the artifacting on the bottom of the foot where the foot
is missing a triangle. The decimation stops once it moves out to
the boundary and corner vertices at the edge of the flat plane,
otherwise there would be fewer triangles still. Performing a
second step of decimation after smoothing also helps remove triangles
(once the edges are not so sharp). Currently, the decimator can
remove roughly 50% of the triangles with minimum artifacting and no
perceptible effect on overall shape. However, due to artifacting,
our final models are not currently decimated.
You might have noticed that these
feet are red.











