Final Results
Integer Linear Programming: What? Why? How?
Advisor: Layla Oesper
Background
Integer linear programming (ILP) is a type of optimization problem. In this setup, variables are integers and are constrained by a set of linear constraints. In particular, one wishes to find a setting of the integer variables, that adheres to all constraints, that additionally maximizes/minimizes a linear function of some or all variables. Many common computer science problems can be formulated as an instance of an ILP including maximum clique-finding in a graph or even the traveling salesperson problem that aims to find the shortest path on a graph that visits all vertices once before returning to the starting vertex. While solving a generic ILP problem has been shown to be computationally intensive (NP-hard), many highly engineered and specialized solvers have been developed that work well in practice. Thus, ILP approaches have been shown to be particularly useful for solving computationally intensive (NP-hard) problems for restricted amounts of input or data.
In particular, the computational biology community has fully embraced the ILP paradigm for solving complex biological problems when no efficient algorithm exists. Examples of biological problems that have been solved using ILPs include RNA-folding prediction and identification of phylogenetic trees describing cancer evolution, among numerous other applications. In particular, many applications in Biology are related to the fact that numerous graph-based problems can be formulated as ILPs.
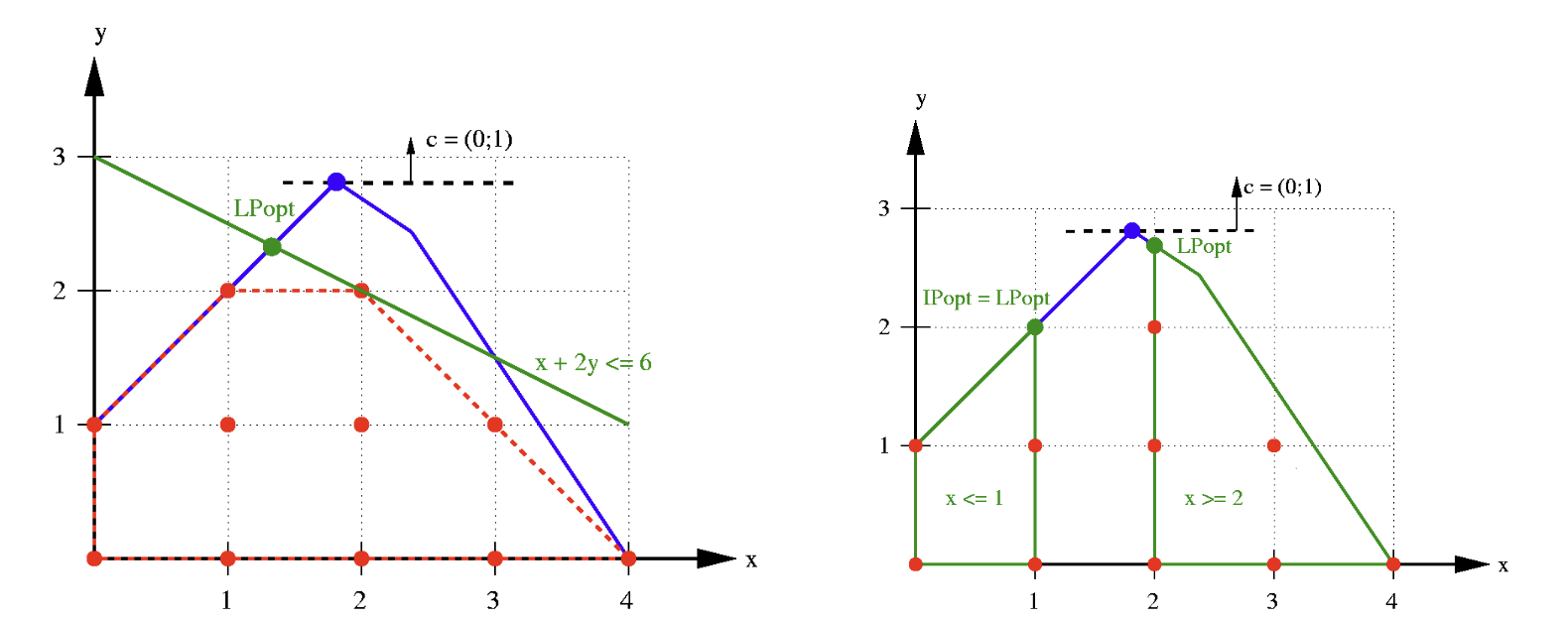
Figure shows two categories of approaches for solving ILP formulations.
The project
In this project you will investigate Integer Linear Programming (ILP). In particular you will:
- Understand the basics of what an ILP is and how it relates to similar problems (e.g., linear programming, binary integer linear programming, and mixed integer linear programming).
- Be able to formulate accurate ILPs (while minimizing the number of constraints used) for a given problem that can be solved by one. In particular, you will do this for various problems in Biology.
- Understand the basics of algorithms used to solve ILPs (e.g. cutting-plane algorithms, branch and bound algorithms etc.).
- Be able to implement and compare ILP formulations using one or more existing ILP solvers.
- Explain why ILPs are useful for solving computationally challenging problems.
Recommended experience
Previous biology experience is NOT required for this project. Other courses that could be useful for this project include linear algebra, algorithms, comp & comp, and computational biology.
References/inspiration
Below are a few textbooks containing content about Integer Linear Programming. These are only intended to provide you a minimal start for your literature search - they are certainly not the only nor necessarily the best sources for ideas. You will be finding and reading many additional papers!
- Dan Gusfield. “Integer Linear Programming in Computational and Systems Biology.” Cambridge University Press, 2019.
- Wayne Winston. “Operations Research: Applications and Algorithms.” Cengage Learning, 4th Edition, 2003.
Meeting Time(s)
Fall Term, MWF 5A