CS 254: Automata and Computability
Takehome exam. Due on paper (except for #7, which should be submitted via your Courses hand-in folder) by 3:00PM Wednesday, 25 May 2011.
This is an open-notes, open-Internet, open-book exam. The only thing you aren't allowed to do is consult with other people about the exam (except for Jeff Ondich, with whom you may discuss the exam as much as you like).
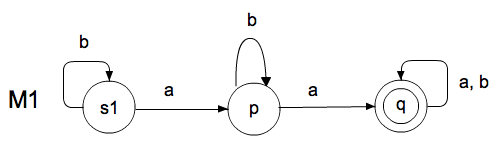
(8 points) Prove that every regular language is also a context-free language by describing a procedure for converting any DFA into an equivalent PDA. Then demonstrate your procedure by applying it to the DFA M1:
- (8 points) Prove that every regular language is also a context-free language by describing a procedure for converting any regular expression into an equivalent context-free grammar, without first converting the regular expression into a finite automaton. Demonstrate your procedure by applying it to the regular expression "(ab)*(a+b)"
- Create a push-down automaton P for which L(P) = {aibjck | i = j + k}. Your write-up should specify Q, Σ, Γ, the start state, the acceptance criterion (empty stack or final state), F (if you use final state acceptance), and δ.
(8 points) Turing machines are normally used to talk about the languages they accept. But they can also perform operations that look like the things we normally think of as computation, regardless of acceptance or rejection. For example, the many string operations that you'll find in the string libraries in most programming languages (replace, find, substring, reverse, s[k], etc.) can be simulated in a Turing machine.
For this problem, you will write a Turing machine with input alphabet Σ = {a, b} that deletes all the b's in the input string, moving all the a's down to fill in the gaps, and then moves to the first blank character before entering the accept state (and thus "shutting down"). For example, if the input string is abbabab (that is, the tape starts with contents ⊦abbabab_ω), then when the machine finishes, the tape should contain ⊦aaa_ω.
(8 points) On page 195 of your textbook, Kozen describes techniques for proving closure properties for CFLs by combining their corresponding CFGs in clever ways. For this problem, you will do something similar by combining PDAs rather than CFGs.
In particular, suppose A1 and A2 are the languages accepted by the PDAs P1 and P2, respectively. Prove that CFLs are closed under concatenation by showing how to construct a PDA P for which L(P) = A1A2.
(8 points) Do problem 89 on page 337 of Kozen.
(8 points) Modify your CKY parser to do the following:
If a context-free grammar is able to generate more than one distinct parse tree for a string (starting with the grammar's start symbol S), the grammar is said to be ambiguous. For example, the grammar in the fifth assignment is ambiguous, as illustrated by the fact that there were two different parse trees rooted at S for the string baaba.
- If the given grammar is able to produce two or more distinct parse trees (starting with the start symbol S) for the given input string, print "Ambiguous parse". (For example, the grammar in the fifth homework assignment is ambiguous, illustrated by the fact that it generates two distinct parse trees rooted at S for the string baaba.)
- Print out a leftmost derivation of the input string in the given grammar.
Your original CKY parsers will be graded by Monday.
Please call your program problem7.py (or problem7.java if you wrote your parser in Java).

Randall Munroe of course, http://xkcd.com/205/